AI models for science are often trained to make predictions about the workings of nature, such as predicting the structure of a biomolecule or the properties of a new solid that can become the next battery material. These tasks require high precision and accuracy. What makes AI for science even more challenging is that highly accurate and precise scientific data is often scarce, unlike the text and images abundantly available from multiple resources.
Given the high demand for solutions and limited resources, researchers turn to innovative approaches such as embedding the laws of nature into AI models, increasing their accuracy, and reducing their reliance on data.
One such approach that gained success last year is embedding the symmetry of the scientific problem into the AI model. Popularized under equivariant neural networks (ENNs), these neural network architectures are built using the mathematical concept of equivariance under symmetry-related transformations.
In simple terms, ENNs are designed to be aware of the underlying symmetries of the problem. For example, if the input to an ENN is rotated, the output will also rotate correspondingly. This means the model can recognize the same object or pattern even if presented in different orientations.
To understand this concept better, consider how ENNs are mostly used today to maintain the relationship between input and output upon symmetry operations in 3D. For example, if an ENN takes a 3D model of a molecule as input and predicts its properties as output, it can predict the same properties for any rotated version of the molecule without needing additional training data or data augmentation. The ENN “understands” that rotating the molecule doesn’t change its fundamental properties (Figure 1).
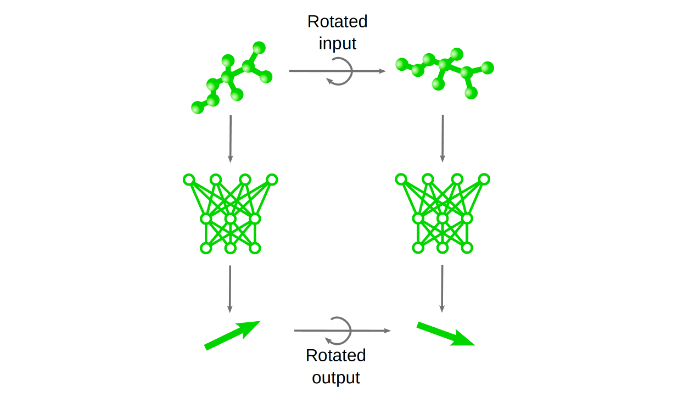
Introducing such fundamental symmetries of nature into network architecture enables models to be more robust and more data-efficient when changes in input data are made. Similar to other strategies of embedding natural laws into neural networks, it also provides a way to increase generalizability to unseen data.
All these benefits come at a cost: constructing ENNs is not theoretically straightforward, and resulting networks are computationally more expensive than their non-equivariant versions. In this post, we describe how the new math library NVIDIA cuEquivariance tackles both challenges and accelerates AI for science models, with examples from drug discovery and material science applications.
Challenges of equivariant neural networks
Many AI models—including Tensor Field Networks, LieConv, Cormorant, SE(3)-Transformer, NequIP, and others like DiffDock and Equiformer—use a unique approach to ensure that they handle changes in input data consistently. They use the basic elements of a symmetry group called irreducible representations (irreps) or variations of these elements. These irreps are mathematically represented as tensors, and they are combined in specific ways, often involving tensor algebra such as tensor products, to make sure the model’s output appropriately reflects any symmetrical transformations applied to the input.
One bottleneck in adopting ENNs that use irreps has been the theoretical complexity of building and working with these irrep objects for a given symmetry group. Lack of existing primitives or extensible APIs combined with theoretical complexity have made it challenging to innovate with ENNs using the irreps formalism. Reusing existing implementations even when they are not optimal has been the more accessible choice in the field.
Furthermore, there are computational complexities when working with irreps-based ENNs. The mathematical foundations determine matrix representations of irreps. For the most used symmetry operations, such as rotations in 3D, these sizes can be unusual for computational optimization, such as 5×5 or 7×7 matrices. This does not allow for leveraging existing optimization techniques, such as tensor cores in mathematical operations, with these objects out of the box.
More importantly, the tensor product operations that involve irreps follow an unusual sparsity pattern rooted in group theory, even though irreps themselves are dense. Irreps have special mixing coefficients called Clebsch-Gordan coefficients that determine how two different irreps can be combined into an output irrep in algebraic operations.
For example, multiplying two irreps can only lead to a specific, limited list of output irreps, and this selection rule is dictated by group theory. Indeed, many combinations of irreps are not allowed due to the selection rule, resulting in sparse Clebsch-Gordan coefficients, most of which are zero. From a computational standpoint, ignoring the sparsity dictated by group theory results in wasted memory and inefficient algorithms.
Accelerating equivariant neural networks
To address these challenges, NVIDIA developed the new cuEquivariance math library that introduces CUDA-accelerated building blocks for equivariant neural networks. cuEquivariance is now available as a public beta on GitHub and PyPi.
The cuEquivariance Python frontend introduces a unified framework called the Segmented Tensor Product (STP) that organizes the algebraic operations with irreps, considering the sparsity pattern of mixing coefficients mentioned earlier. STP generalizes the computation of equivariant multilinear products, enabling the user to express a wide range of such operations between irreps. It also gives the user the freedom to define operations that are not necessarily equivariant, which may be helpful for applications that are not yet explored in the research community.
Building on the STP framework, cuEquivariance utilizes specialized CUDA kernels to accelerate the most commonly used instances of STPs. Most of the bottleneck operations in ENNs are multiple memory-bound operations performed one after another, resulting in unnecessary loading and storing of intermediates. Given the small size of irreps and their high number, performing each operation with a distinct kernel call is another source of overhead. cuEquivariance uses kernel fusion to replace these individual operations with a few special-purpose GPU kernels.
Beyond kernel fusion, the memory layout of features is restructured such that memory access maps better to the Single Instruction, Multiple Threads (SIMT) paradigm of NVIDIA GPU architecture. This specialized backend is optimized for performance on NVIDIA GPUs, enabling significant speedups in math operations within equivariant neural networks.
Figure 2 shows the impact of cuEquivariance acceleration on two popular AI for science models: DiffDock, a diffusion model that predicts the protein-ligand binding pose, and MACE, a machine-learned interatomic potential that is used extensively in materials science and biology to govern molecular dynamics simulations.
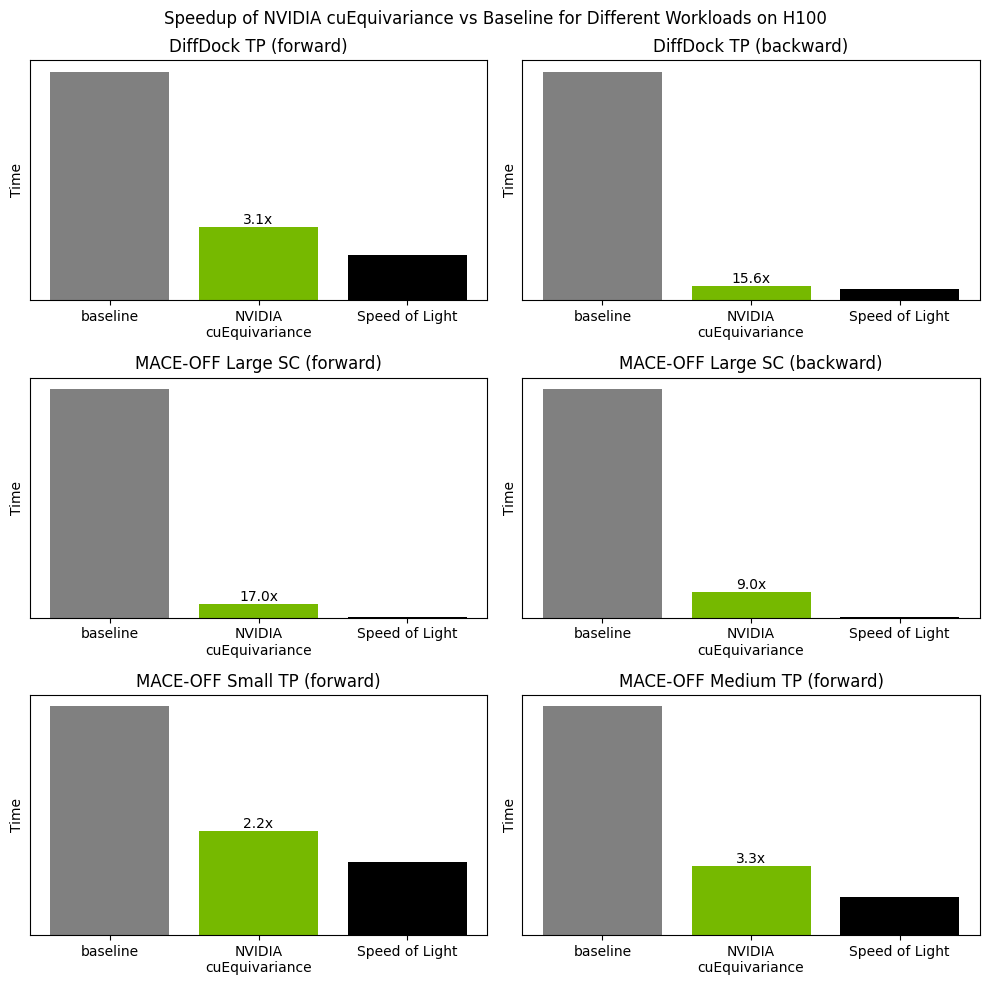
These equivariant neural network models have multiple tensor operations with irreps. For demonstration purposes, the computationally most demanding operations for each model are selected. For DiffDock, this is an irrep-based tensor product operation (TP). For MACE, two operations that impact performance are considered: Symmetric Contraction (SC), a tensor contraction of an irreps tensor with itself, and TP, similar to that of DiffDock. For each operation, forward and backward performance are shown.
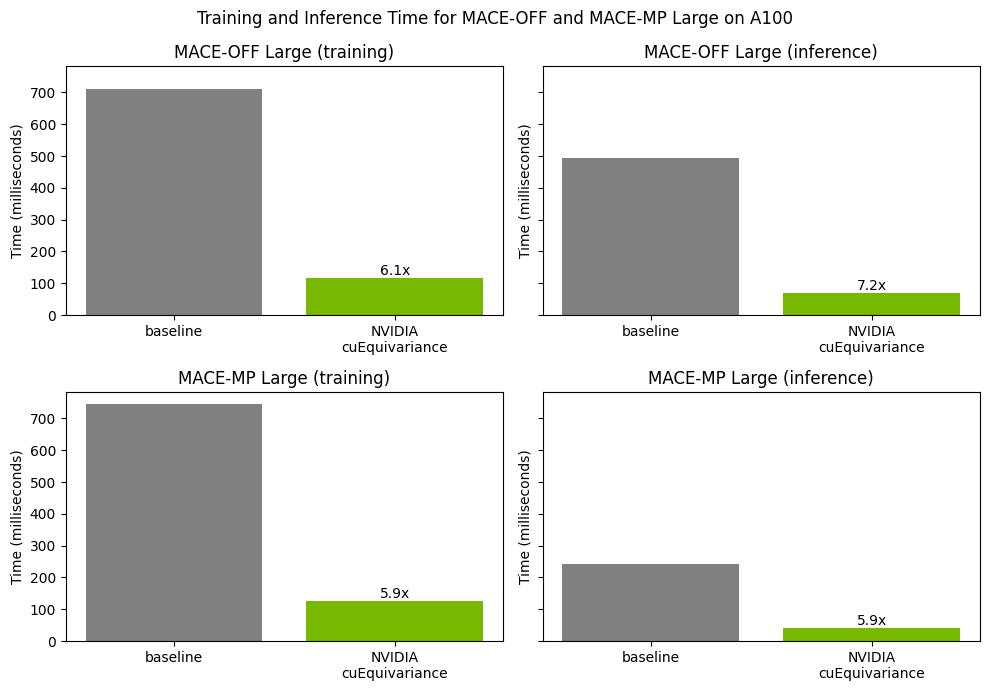
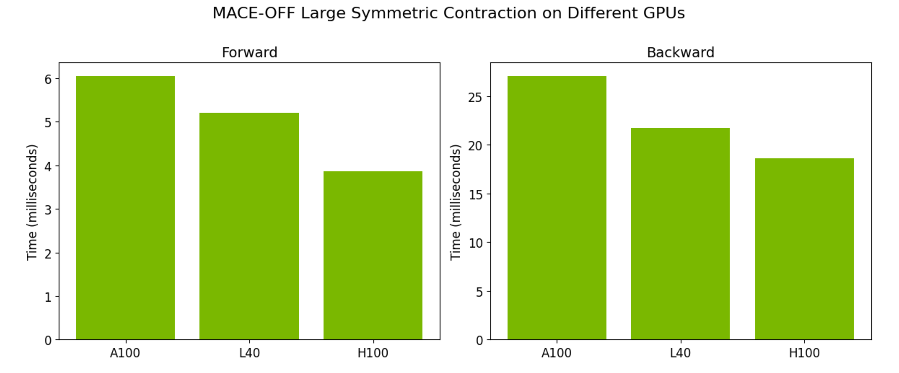
Figure 3 presents the end-to-end performance of MACE-OFF Large and MACE-MP Large models with cuEquivariance. Finally, Figure 4 shows how the performance changes across different NVIDIA GPUs.
Conclusion
The development of cuEquivariance marks a significant step forward in accelerating AI for science. By addressing the theoretical and computational challenges of equivariant neural networks, cuEquivariance empowers researchers, scientists, and academics to build more accurate, efficient, and generalizable models for various scientific applications. As demonstrated by its successful integration into widely used models like DiffDock and MACE, cuEquivariance is poised to drive innovation and accelerate discoveries in fields like drug discovery, materials science, and beyond.
By harnessing the power of symmetry and efficient computation, cuEquivariance unlocks new possibilities for AI to contribute to scientific breakthroughs. Combining open-source accelerated computing tools such as cuEquivariance with systematically generated, large-scale datasets can improve the accuracy performance of AI models, fostering broader adoption and integration in research and enterprise products.
Get started with cuEquivariance.